Si
deseas compartir
esta pagina
con tus amigos, compañeros de escuela o familia, simplemente da
click aqui
E
N L A C E S
Informacion
Financiera
Sistemas
de Contabilidad
Introduccion
a los Costos
Definicion
de Costo
Uso
de los Costos
Clasificacion
de los Costos
Valuacion
de Inventarios
Comportamiento
de los Costos
Sistemas
de Costos
Costos
Estandar y Varianzas
Analisis
Costo-Volumen-Utilidad
Punto
de Equilibrio
Utilidad
Deseada
Presupuesto
Presupuesto
Maestro
Costeo
Basado en Actividades
Precios
de Transferencia
Menu Principal
Bibliografia
Contacto
Articulos Interesantes
con tus amigos, compañeros de escuela o familia, simplemente da
click aqui
Menu Principal
Bibliografia
Contacto
Articulos Interesantes
Métodos para segmentar los costos semivariables
Si se expresaran algebraicamente, los costos semivariables estarían representados por la siguiente ecuación:
CSV = a + bx
En donde: CSV = Costos semivariables
a = Costos fijos
b = Tasa de costos variables
x = Generador de costo (unidades, horas máquina, horas de mano de obra, etcétera).
Uno de los grandes retos de un administrador en cuanto a los costos semivariables es la estimación de los segmentos fijos y variables del costo. Para llevar a cabo dicha segmentación, existen diferentes métodos con mayor o menor grado de exactitud, los cuales pueden clasificarse en cuatro categorías:
1. Métodos de estimación directa.
2. Método punto alto-punto bajo.
3. Métodos a través de diagramas de dispersión.
4. Métodos estadísticos (correlación).
No hay un método de segmentación útil para todas las circunstancias o partidas de costos de una empresa; cada una debe utilizar el que considere más apropiado. Estos métodos se aplican a las partidas semivariables, es decir, aquellas que quedaron después de clasificar las partidas puramente fijas o variables en las que se requiere separar la porción fija y variable.
1. Métodos de estimación directa: Estos métodos se aplican en ciertos casos específicos, concretos, y generalmente no son adaptables a partidas ordinarias.2 Cabe destacar que estos métodos son aplicables en casos específicos, como por ejemplo, cuando existe alguna partida que por su naturaleza no puede estar sujeta a análisis estadístico; cuando se crean nuevos departamentos que originen costos; cuando se adquiere nuevo equipo o maquinaria que origine un costo; o cuando se producen cambios en los métodos. Dentro de este grupo tenemos los siguientes métodos:
a) Basados en estudio de tiempos y movimientos: Se aplican cuando no se tiene un buen registro de costos históricos o cuando se trata de una situación nueva en la organización. Ante dicha circunstancia, mediante observaciones de ingeniería industrial, se detecta el comportamiento de las nuevas partidas que surgen.
b) Basados en el análisis de la administración de los datos históricos: En este caso el analista determina el comportamiento de los costos en función del análisis de costos históricos; de la interpretación de las políticas administrativas respecto a dicha partida; y de la experiencia profesional subjetiva.
2. Método punto alto-punto bajo: Este enfoque se basa en la estimación de la parte fija y de la parte variable de un costo en dos diferentes niveles de actividad, las cuales son calculadas a través de una interpolación aritmética entre los dos diferentes niveles. Retomando la ecuación de costos semivariables CSV 5 a 1 bx, esta interpolación nos dará como resultado la pendiente de la línea que representa la tasa de costos variable (o sea, b) y la parte en que dicha línea intercepta el eje Y (costo fijo o a). Este método parte de varios supuestos:
• Se considera que los puntos más altos y más bajos del costo son los más representativos para explicar el comportamiento habitual de los costos de la empresa.
• Existe una relación lineal entre los costos variables y los generadores que impulsan ese costo.
• No existen factores estacionales que afecten positiva o negativamente el comportamiento lineal de los costos variables o fijos.
La gran ventaja de este método es que resulta muy sencillo de calcular, ya que no requiere cálculos complejos o paquetes computacionales.
A continuación se presenta la metodología para calcular la función de costos semivariables utilizando el método punto alto-punto bajo:
a) Seleccionar la actividad que servirá como denominador, que puede ser horas-máquina, horas de mano de obra, etc., según se considere apropiado.
b) Identificar el nivel relevante dentro del cual no hay cambios de los costos fijos; dicho nivel se refiere a la capacidad instalada dentro de la cual no se requerirán cambios en los costos fijos.
c) Determinar el costo total en los dos niveles.
d) Determinar el valor de la tasa de costo variable (“b” ), utilizando el cálculo tradicional para obtener la pendiente de una función lineal. Adaptándolo al método, este cálculo sería como sigue:
Costo mas alto - Costo mas bajo
b = ----------------------------------------------------------------------
Nivel de actividad mas alto - Nivel de actividad mas bajo
b = ----------------------------------------------------------------------
Nivel de actividad mas alto - Nivel de actividad mas bajo
Es
importante mencionar que al
llevar a cabo esta selección, exista una coherencia entre los costos y
el nivel de actividad. De esta manera, el nivel de actividad más alto
deberá estar relacionado con el costo más alto de la muestra, y el
nivel de actividad más bajo deberá arrojar el costo más bajo en la
muestra. Si esta pequeña regla no se cumple (es decir, que el costo más
alto no corresponda el nivel de actividad más alto y viceversa),
la muestra obtenida no servirá para llevar a cabo la estimación, puesto
que implica que no existe una relación proporcional entre
el nivel de actividad y el costo.
e) Determinar el valor del costo fijo de la ecuación (“a” ), recurriendo a la tasa de costos variables (“b” ) obtenida en el paso anterior. Para determinar el componente fijo del costo semivariable, se toma el costo más alto y se le resta el costo variable total que de acuerdo con la tasa de costos variable debe haber al nivel más alto de actividad, de la siguiente manera:
En donde:
a = Costo fijo
CSVmáx = Costo semivariable máximo
b = Tasa de costo variable
Xmáx = Nivel de actividad máximo
Una vez obtenido el componente fijo y variable, es posible expresar la ecuación de la manera que se describió anteriormente:
CSV = a + bx
Para ejemplificar el uso del método punto alto-punto bajo, se presenta a continuación una muestra de los costos por energéticos de los últimos cinco meses a fin de determinar su ecuación de costos:

e) Determinar el valor del costo fijo de la ecuación (“a” ), recurriendo a la tasa de costos variables (“b” ) obtenida en el paso anterior. Para determinar el componente fijo del costo semivariable, se toma el costo más alto y se le resta el costo variable total que de acuerdo con la tasa de costos variable debe haber al nivel más alto de actividad, de la siguiente manera:
a = CSVmáx - b (Xmáx)
En donde:
a = Costo fijo
CSVmáx = Costo semivariable máximo
b = Tasa de costo variable
Xmáx = Nivel de actividad máximo
Una vez obtenido el componente fijo y variable, es posible expresar la ecuación de la manera que se describió anteriormente:
CSV = a + bx
Para ejemplificar el uso del método punto alto-punto bajo, se presenta a continuación una muestra de los costos por energéticos de los últimos cinco meses a fin de determinar su ecuación de costos:

En primer lugar, debemos determinar la tasa del costo
variable o (b) del costo de energéticos, de la manera siguiente:
Cmax
- Cmin
$1 600 000 - $1
200 000
b = ------------------- = --------------------------------- = $2 / hm
Xmax - Xmin 300 000 - 200 000
b = ------------------- = --------------------------------- = $2 / hm
Xmax - Xmin 300 000 - 200 000
En donde:
b = Tasa de costo variable
Cmáx/Cmín = Costo máximo/Costo mínimo
Xmáx/Xmín = Nivel de actividad máximo/mínimo
Ahora se calculará la parte fija usando el nivel máximo de 300 000 horas-máquina, cuyo costo total es $1 600 000.
En donde:
a = Costos fijos
b = Tasa de costos variable
Cmáx = Costos máximos
Xmáx = Nivel de actividad máximo
El resultado es el monto de los costos fijos que, según se supone, no se alteran dentro del tramo de 100 000 hasta 300 000 horas-máquina, lo cual puede ser probado en cualquier nivel dentro del tramo relevante. Este método es sumamente sencillo y resulta aplicable en condiciones en las que la variación del costo fijo no sea significativa.
Es importante destacar que la parte fija (a) en la ecuación costo semivariable respeta la periodicidad de la muestra utilizada para obtenerla, esto es, si la muestra fue mensual, el costo fijo estimado es también mensual y así sucesivamente. Esta situación se presenta en cualquiera de los métodos de estimación que analizamos en esta pagina.
3. Métodos a través de diagramas de dispersión: Este método es de gran utilidad para complementar el método punto alto-punto bajo, que con frecuencia utiliza dos puntos que no necesariamente son representativos de la función de costos que se está analizando para determinar su comportamiento. De esta manera, este método permite a la administración seleccionar dos puntos representativos de la función de costos que se analiza. Incluso si se concluyera que estos dos puntos no son representativos, se pueden seleccionar otros dos que lo sean, gracias a la forma gráfica que permite, visualmente, efectuar una buena selección.
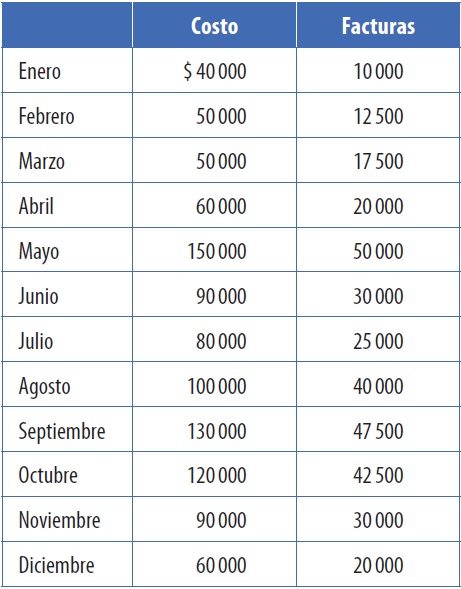
El primer paso para utilizar este método es señalar en la gráfica el costo que se genera en cada uno de los diferentes niveles de actividad; en el eje horizontal se señalan los diferentes niveles de actividad y en el eje vertical los diferentes costos. Observando la gráfica se puede suponer que el comportamiento de esta función de costos es lineal, por lo cual es importante seleccionar dos puntos que representen bien dicha función lineal, lo que constituye la gran ventaja respecto al método de punto alto-punto bajo. Supongamos los siguientes datos:
b = Tasa de costo variable
Cmáx/Cmín = Costo máximo/Costo mínimo
Xmáx/Xmín = Nivel de actividad máximo/mínimo
Ahora se calculará la parte fija usando el nivel máximo de 300 000 horas-máquina, cuyo costo total es $1 600 000.
a = Cmax - b (Xmax)
a = 1 600 000 - 2 (300 000)
a = 1 600 000 - 2 (300 000)
a = 1 000 000
En donde:
a = Costos fijos
b = Tasa de costos variable
Cmáx = Costos máximos
Xmáx = Nivel de actividad máximo
El resultado es el monto de los costos fijos que, según se supone, no se alteran dentro del tramo de 100 000 hasta 300 000 horas-máquina, lo cual puede ser probado en cualquier nivel dentro del tramo relevante. Este método es sumamente sencillo y resulta aplicable en condiciones en las que la variación del costo fijo no sea significativa.
Es importante destacar que la parte fija (a) en la ecuación costo semivariable respeta la periodicidad de la muestra utilizada para obtenerla, esto es, si la muestra fue mensual, el costo fijo estimado es también mensual y así sucesivamente. Esta situación se presenta en cualquiera de los métodos de estimación que analizamos en esta pagina.
3. Métodos a través de diagramas de dispersión: Este método es de gran utilidad para complementar el método punto alto-punto bajo, que con frecuencia utiliza dos puntos que no necesariamente son representativos de la función de costos que se está analizando para determinar su comportamiento. De esta manera, este método permite a la administración seleccionar dos puntos representativos de la función de costos que se analiza. Incluso si se concluyera que estos dos puntos no son representativos, se pueden seleccionar otros dos que lo sean, gracias a la forma gráfica que permite, visualmente, efectuar una buena selección.
El primer paso para utilizar este método es señalar en la gráfica el costo que se genera en cada uno de los diferentes niveles de actividad; en el eje horizontal se señalan los diferentes niveles de actividad y en el eje vertical los diferentes costos. Observando la gráfica se puede suponer que el comportamiento de esta función de costos es lineal, por lo cual es importante seleccionar dos puntos que representen bien dicha función lineal, lo que constituye la gran ventaja respecto al método de punto alto-punto bajo. Supongamos los siguientes datos:

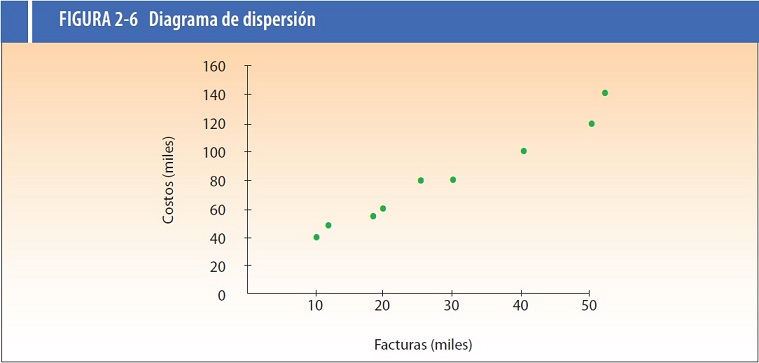
Al observar el diagrama de
dispersión en la figura 2-6 se
pueden elegir los puntos que representan correctamente la relación
entre el costo y la actividad que da origen o detona el consumo de
dicho insumo. Este método se enriquece aún más cuando se aprovecha la
experiencia de los administradores en la selección de los dos puntos
que reflejen correctamente el comportamiento de los costos en la
partida que se está analizando. Utilizando la información proporcionada
previamente, se supondrá que los administradores seleccionan lo
ocurrido en enero y junio porque son los meses más representativos de
acuerdo con la experiencia de otros años; por ello, la línea debe pasar
por los puntos 1 y 6. De acuerdo con ello, vemos cómo se calcula la
parte de costo fijo y el costo variable por factura emitida.
El costo y las facturas de enero son: $40 000 10 000
El costo y las facturas de junio son: $90 000 30 000
De donde el costo variable por factura será:
El costo y las facturas de enero son: $40 000 10 000
El costo y las facturas de junio son: $90 000 30 000
De donde el costo variable por factura será:
C2 - C2
$90 000 - $40 000
b = ------------ = --------------------------- = $2.50 / hm
X2 - X1 30 000 - 10 000
b = ------------ = --------------------------- = $2.50 / hm
X2 - X1 30 000 - 10 000
Donde:
b = Costo variable
C = Costo total
X = Volumen
Por lo tanto, si el costo variable por factura es $2.50, la parte de costos fijos del total del costo de enero sería:
b = Costo variable
C = Costo total
X = Volumen
Por lo tanto, si el costo variable por factura es $2.50, la parte de costos fijos del total del costo de enero sería:
a = CSV1
- b (X1)
a = 40 000 - (2.5) (10 000)
a
= $15 000a = 40 000 - (2.5) (10 000)
Donde:
CSV1 = Costo semivariable al nivel de actividad 1
a = Costo fijo
b = Costo variable por factura
X = Nivel de actividad 1
CSV1 = Costo semivariable al nivel de actividad 1
a = Costo fijo
b = Costo variable por factura
X = Nivel de actividad 1

Por lo tanto, dentro
del rango de
10 000 a 47 500 facturas, el costo variable unitario por factura es
$2.50 y el costo fijo es de $15 000. De lo anterior se concluye que,
dentro de este rango, puede predecirse el costo del total de emisión de
facturas, cualquiera que sea el número de facturas emitidas.
Siempre se podrá cuestionar si los dos puntos seleccionados son los correctos, pero por ello se puede afirmar que la calidad de la información obtenida sobre el comportamiento de los costos depende del juicio con que la administración elija los dos puntos y efectúe su análisis. También es cierto que al usar el método punto alto-punto bajo en un mismo nivel de emisión de facturas para determinar el costo total, el resultado va a ser diferente si se utiliza el método de diagrama de dispersión. La pregunta obligada es: ¿cuál de los dos es el correcto? La respuesta es que, definitivamente, el método de diagrama de dispersión, que permite visualmente escoger dos puntos representativos, es menos subjetivo que el método punto alto-punto bajo; sin embargo, si se quiere reducir aún más la subjetividad, lo mejor es utilizar el método de mínimos cuadrados, utilizando correlación simple o múltiple, que se analizará a continuación.
4. Métodos estadísticos: El análisis de regresión es una herramienta estadística que sirve para medir la relación entre una variable dependiente y una o más variables independientes.
La relación entre una variable dependiente y una independiente se llama regresión simple; si la relación es entre una variable dependiente y varias independientes, se denomina regresión múltiple. Este análisis trata de mostrar la relación entre ambas variables y la manera en que las variables independientes repercuten en la dependiente; dichos efectos serán expresados en forma de ecuación. Se utilizará el análisis de regresión para calcular el comportamiento de las partes variables y fijas de cualquier partida de costos. Una manera de expresar esta relación simple es:
Siempre se podrá cuestionar si los dos puntos seleccionados son los correctos, pero por ello se puede afirmar que la calidad de la información obtenida sobre el comportamiento de los costos depende del juicio con que la administración elija los dos puntos y efectúe su análisis. También es cierto que al usar el método punto alto-punto bajo en un mismo nivel de emisión de facturas para determinar el costo total, el resultado va a ser diferente si se utiliza el método de diagrama de dispersión. La pregunta obligada es: ¿cuál de los dos es el correcto? La respuesta es que, definitivamente, el método de diagrama de dispersión, que permite visualmente escoger dos puntos representativos, es menos subjetivo que el método punto alto-punto bajo; sin embargo, si se quiere reducir aún más la subjetividad, lo mejor es utilizar el método de mínimos cuadrados, utilizando correlación simple o múltiple, que se analizará a continuación.
4. Métodos estadísticos: El análisis de regresión es una herramienta estadística que sirve para medir la relación entre una variable dependiente y una o más variables independientes.
La relación entre una variable dependiente y una independiente se llama regresión simple; si la relación es entre una variable dependiente y varias independientes, se denomina regresión múltiple. Este análisis trata de mostrar la relación entre ambas variables y la manera en que las variables independientes repercuten en la dependiente; dichos efectos serán expresados en forma de ecuación. Se utilizará el análisis de regresión para calcular el comportamiento de las partes variables y fijas de cualquier partida de costos. Una manera de expresar esta relación simple es:
Y = a + bx
Donde:
Y 5 Costo total de una partida determinada (variable dependiente)
a 5 Costos fijos (intercepción con el eje de las ordenadas)
b 5 Costo variable por unidad de la actividad en torno a la cual cambia (pendiente de la recta)
x 5 La actividad en torno a la cual cambia el costo variable (variable independiente)
En el caso de regresión simple, la técnica de aplicación para encontrar los valores de ambas variables es la de mínimos cuadrados, cuya mecánica será la siguiente:

Donde:
Y 5 Costo total de una partida determinada (variable dependiente)
a 5 Costos fijos (intercepción con el eje de las ordenadas)
b 5 Costo variable por unidad de la actividad en torno a la cual cambia (pendiente de la recta)
x 5 La actividad en torno a la cual cambia el costo variable (variable independiente)
En el caso de regresión simple, la técnica de aplicación para encontrar los valores de ambas variables es la de mínimos cuadrados, cuya mecánica será la siguiente:

A continuación se
expondrá un ejemplo en el cual se determinará la parte fija y la parte
variable de una partida que corresponde a un costo indirecto de
fabricación: el mantenimiento.
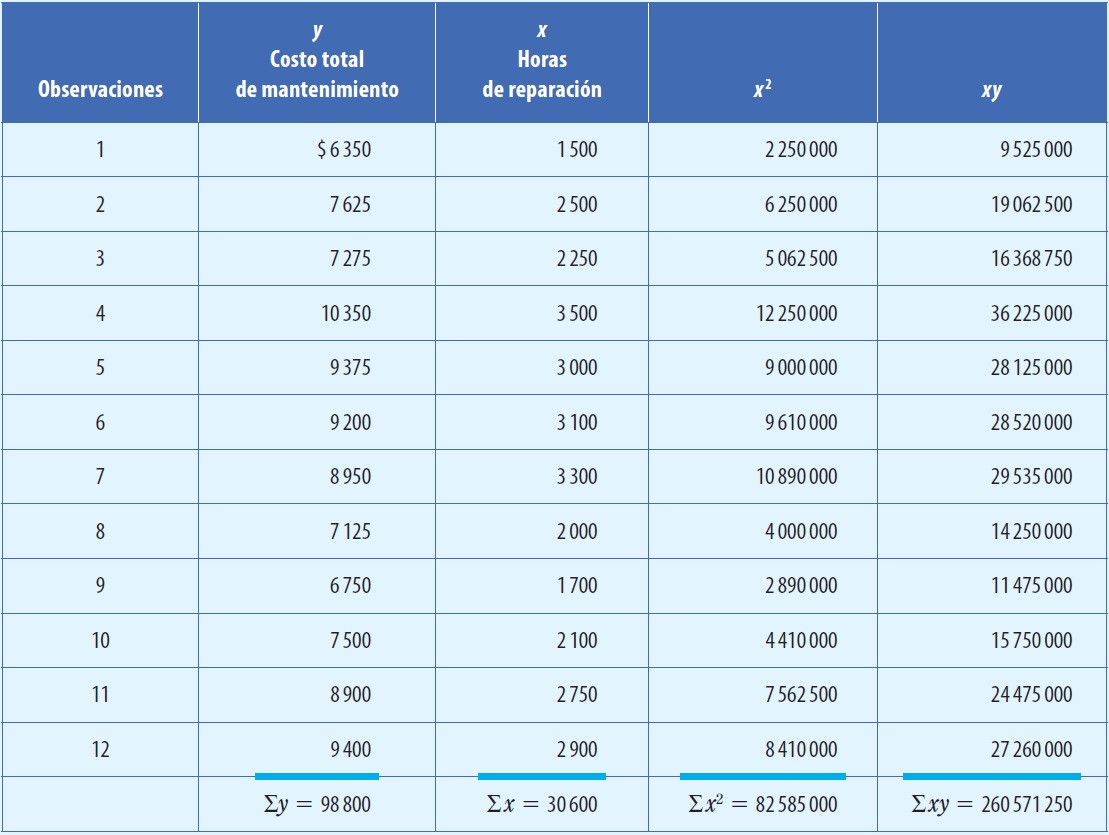

Aplicando las fórmulas (5) y (6)
se obtiene el comportamiento
de los costos:


Sustituyendo los valores se
determinan los costos fijos y
variables:
y = 3 401.35 + 1.895 (x)
Esto quiere decir que los costos fijos del departamento de mantenimiento son $3 401.35 y que el costo variable por hora de reparación es de $1.895, de tal forma que si en el próximo periodo productivo se trabajaran 2 700 horas de mantenimiento, el costo total sería:
Esto quiere decir que los costos fijos del departamento de mantenimiento son $3 401.35 y que el costo variable por hora de reparación es de $1.895, de tal forma que si en el próximo periodo productivo se trabajaran 2 700 horas de mantenimiento, el costo total sería:
CT = 3 401.35 + 1.895 (2 700)
CT = 8 517.85
Es importante que se comprenda claramente esta técnica estadística, pues se aplica de manera exhaustiva en las áreas de contabilidad administrativa, por ejemplo en la simulación de decisiones con el modelo costo-volumen-utilidad, la elaboración del presupuesto de ventas, el desarrollo del presupuesto flexible, etcétera.
CT = 8 517.85
Es importante que se comprenda claramente esta técnica estadística, pues se aplica de manera exhaustiva en las áreas de contabilidad administrativa, por ejemplo en la simulación de decisiones con el modelo costo-volumen-utilidad, la elaboración del presupuesto de ventas, el desarrollo del presupuesto flexible, etcétera.